Top　　関連リンク エントロピーと、断熱・準静的・可逆・不可逆の関係

---

断熱過程のエントロピー変化を別経路で計算してみる

準静的な断熱過程のエントロピー変化(=0) を、別の過程経由(下記)で計算して確認する。
・等温過程 → 定圧過程
・等温過程 → 定積過程
・定圧過程 → 定積過程

考えるのは断熱膨張でも断熱圧縮でもよいが、どちらかに決めておいた方が図が描きやすいので膨張とする。
変数として、温度 T、圧力 p、体積 V、質量 m、気体定数 R、定積比熱 c_v、定圧比熱 c_p、比熱比 κ、内部エネルギー U、熱量 q を用いる。
x の対数を ln(x) と表記する。
最初の状態を 状態1、最後の状態を状態2、途中の過程が切り替わる状態を状態3 とし、変数の添字に用いる。
よって、T₁ > T₂、p₁ > p₂、V₁ < V₂、S_1→2 = 0 である。

等温過程 → 定圧過程

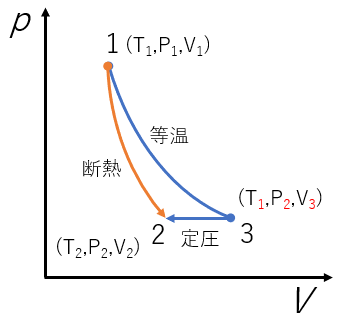
1. 等温過程 (T₁、状態1→状態3)

ボイルシャルルの法則より
　p = p₁V₁ / V

等温過程なので
　dU = 0
　d'q = dU + pdV = pdV
　S_1→3 = ∫d'q / T₁
　 = 1 / T₁ × ∫p dV　(区間 V₁～V₃)
　 = p₁V₁ / T₁ × ∫1 / V dV　(区間 V₁～V₃)
　 = p₁V₁ / T₁ ln (V₃ / V₁)

気体の状態方程式から、
　p₁V₁ / T₁ = mR

よって S_1→3は、
　S_1→3 = mR ln (V₃ / V₁)

ところで、断熱過程(状態1→状態2) ではポアソンの法則から次式が成り立つ。
　 (T₁ / T₂) ^κ/(κ-1) = (p₁ / p₂)

状態1→状態3 でボイルシャルルの法則から、
　V₃ / V₁ = p₁ / p₂
よって、
　V₃ / V₁ = (T₁ / T₂) ^κ/(κ-1)

よって S_1→3は、
　S_1→3 = mR ln (T₁ / T₂) ^κ/(κ-1)
　= mR・κ/(κ-1)・ln (T₁ / T₂)

定圧比熱 c_p と定積比熱 c_p の関係式 c_p = c_v + R = κ c_v から、
　c_p = R κ / (κ - 1)

よって S_1→3は、
　S_1→3 = m c_p ln (T₁ / T₂)

2. 定圧過程 (p₂、状態3→状態2)

ボイルシャルルの法則より
　V = (V₂ / T₂)・T
　dV = (V₂ / T₂)・dT

　d'q = dU + p dV
　 = m c_v dT + p₂ dV
　 = m c_v dT + p₂V₂ / T₂ dT

気体の状態方程式から、
　p₂V₂ / T₂ = mR

よって d'q は、
　d'q = m (c_v + R) dT

　S_3→2 = ∫d'q / T
　 = m (c_v + R) ∫dT / T　(区間 T₁～T₂)
　 = m (c_v + R) ln (T₂ / T₁)

マイヤーの公式より、c_p = R + c_v なので、
　S_3→2 = m c_p ln (T₂ / T₁)

3. 和

　S_1→2 = S_1→3 + S_3→2
　 = m c_p ln (T₁ / T₂) + m c_p ln (T₂ / T₁)
　 = 0

等温過程 → 定積過程

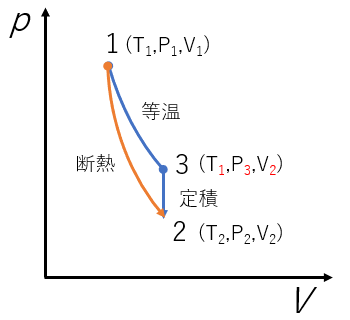
1. 等温過程 (T₁、状態1→状態3)

ボイルシャルルの法則より
　p = p₁V₁ / V

等温過程なので
　dU = 0
　d'q = dU + pdV = pdV
　S_1→3 = ∫d'q / T₁
　 = 1 / T₁ × ∫p dV　(区間 V₁～V₂)
　 = p₁V₁ / T₁ × ∫1 / V dV　(区間 V₁～V₂)
　 = p₁V₁ / T₁ ln (V₂ / V₁)

気体の状態方程式から、
　p₁V₁ / T₁ = mR

よって S_1→3は、
　S_1→3 = mR ln (V₂ / V₁)

2. 定積過程 (V₂、状態3→状態2)

定積過程なので
　p dV = 0
　d'q = dU + pdV = dU
　 = m c_v dT

　S_3→2 = ∫d'q / T
　 = m c_v ∫dT / T　(区間 T₁～T₂)
　 = m c_v ln (T₂ / T₁)

ところで、断熱過程(状態1→状態2) ではポアソンの法則から次式が成り立つ。
　 (T₂ / T₁) = (V₁ / V₂) ^κ-1

よって S_3→2は、
　S_3→2 = m c_v ln (V₁ / V₂) ^κ-1
　 = m c_v (κ-1) ln (V₁ / V₂)

定圧比熱 c_p と定積比熱 c_p の関係式 c_p = c_v + R = κ c_v から、
　R = c_v(κ - 1)

よって S_3→2は、
　S_3→2 = mR ln (V₁ / V₂)

3. 和

　S_1→2 = S_1→3 + S_3→2
　 = mR ln (V₂ / V₁) + mR ln (V₁ / V₂)
　 = 0

定圧過程 → 定積過程

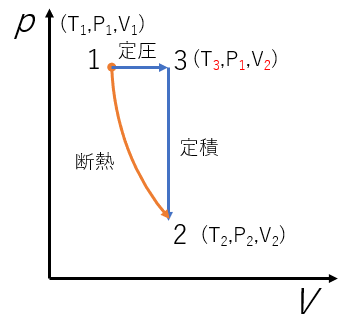
1. 定圧過程 (p₁、状態1→状態3)

気体の状態方程式より、
　p₁ dV = m R dT
　dV = (m R / p₁) dT

　d'q = dU + p₁ dV
　 = m c_v dT + p₁ (m R / p₁) dT
　 = m (c_v + R) dT

　S_1→3 = ∫d'q / T
　 = m (c_v+R) ∫dT / T　(区間 T₁～T₃)
　 = m c_p ln (T₃ / T₁)

ボイルシャルルの法則より、
　T₃ / T₁ = V₂ / V₁

よって S_1→3は、
　S_1→3 = m c_p ln (V₂ / V₁)

2. 定積過程 (V₂、状態3→状態2)

定積過程なので、
　p dV = 0
　d'q = dU + p dV = dU
　 = m c_v dT

　S_3→2 = ∫d'q / T
　 = m c_v ∫dT / T　(区間 T₃～T₂)
　 = m c_v ln (T₂ / T₃)

ボイルシャルルの法則より、
　T₂ / T₃ = p₂ / p₁

よって S_3→2は、
　S_3→2 = m c_v ln (p₂ / p₁)

ところで、断熱過程(状態1→状態2) ではポアソンの法則から次式が成り立つ。
　 (p₂ / p₁) = (V₁ / V₂) ^κ

よって S_3→2は、
　S_3→2 = m c_v ln (V₁ / V₂) ^κ
　 = m κ c_v ln (V₁ / V₂) 　 = m c_p ln (V₁ / V₂)

3. 和

　S_1→2 = S_1→3 + S_3→2
　= m c_p ln (V₂ / V₁) + m c_p ln (V₁ / V₂)
　= 0

まとめ

エントロピー以外に、熱量・仕事・内部エネルギーを含めた表。
式は、T₃、p₃、V₃ が消える形に整理している。

過程		熱量 Q	仕事 W	内部エネルギー ΔU	エントロピー ΔS
断熱過程 (1→2)		0	m cv (T1 - T2)	m cv (T2 - T1)	0
等温過程 ↓ 定圧過程	等温過程 (1→3)	m cp T1 ln (T1 / T2)	m cp T1 ln (T1 / T2)	0	m cp ln (T1 / T2)
	定圧過程 (3→2)	m cp (T2 - T1)	m R (T2 - T1)	m cv (T2 - T1)	m cp ln (T2 / T1)
等温過程 ↓ 定積過程	等温過程 (1→3)	m R T1 ln (V2 / V1)	m R T1 ln (V2 / V1)	0	m R ln (V2 / V1)
	定積過程 (3→2)	m cv (T2 - T1)	0	m cv (T2 - T1)	m R ln (V1 / V2)
定圧過程 ↓ 定積過程	定圧過程 (1→3)	m cp T1 (V2 / V1 - 1)	m R T1 (V2 / V1 - 1)	m cv { (V2 / V1)T1 - T1 }	m cp ln (V2 / V1)
	定積過程 (3→2)	m cv { T2 - (V2 / V1)T1 }	0	m cv { T2 - (V2 / V1)T1 }	m cp ln (V1 / V2)