Top

---

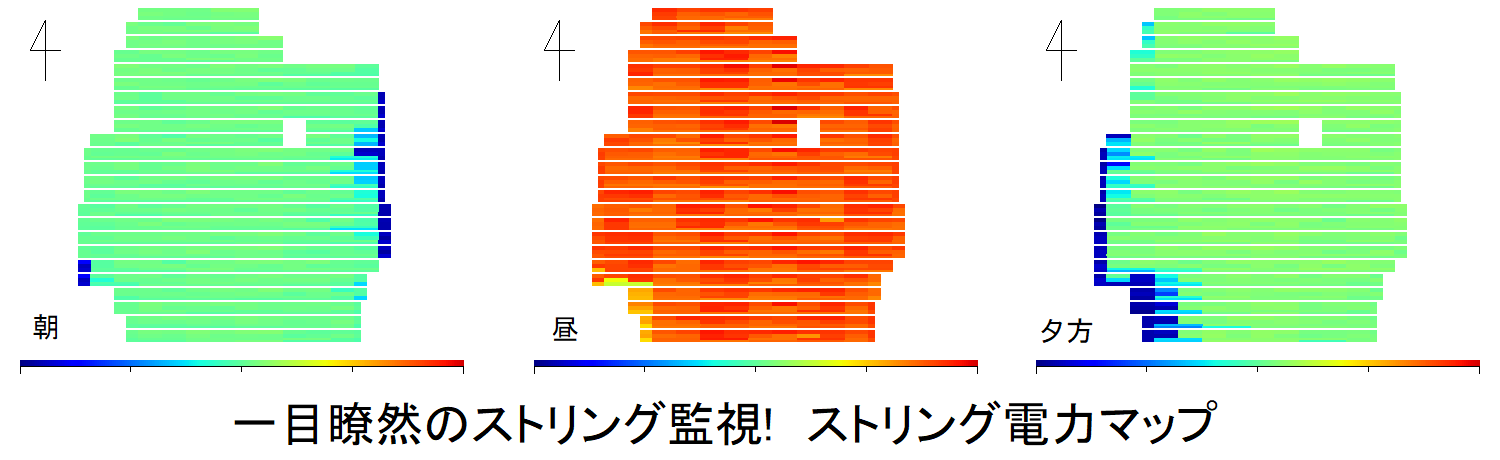
ソーラーパネルに影ができないための条件　地面の傾斜とパネルの傾斜とパネル間距離の関係

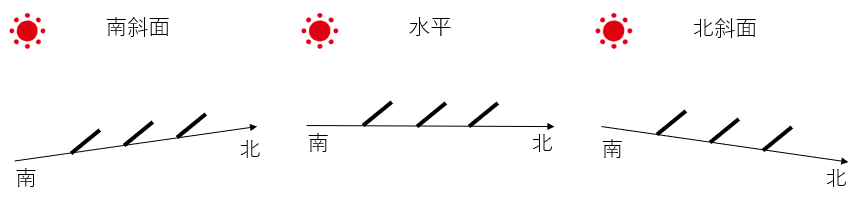
太陽光パネルを複数列に並べる場合に、隣の列のパネルに影が落ちない条件を計算する。
パネルは南向きに傾斜をつけて設置されているものとする。
大地の傾きは、水平・南傾斜・北傾斜を考慮する。
パネルの南端(一番低いところ)の高さを 0 として計算するが、0 でない場合でも全パネルが一様に高くなるだけなので、
パネルが別のパネルに影を落す条件には影響しない。よって南端の高さが 0でない場合にも適用できる。

軸と変数の定義

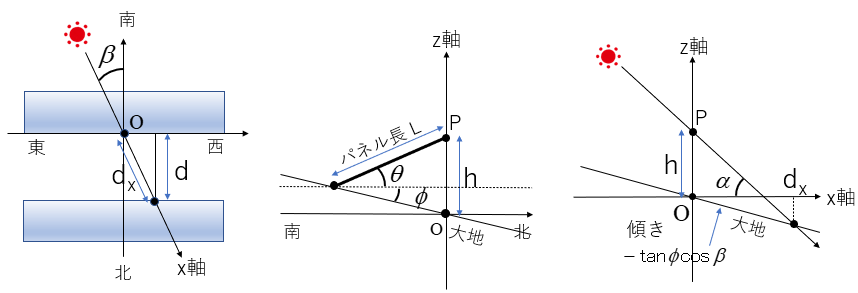
パネルの長さを L、水平に対するパネルの角度を θ、隣りの列との距離を d とする。
太陽の仰角を α、太陽の方位角を β とする。方位角は南を 0、東を正とする。
大地の南北方向の傾斜角を φ とする。傾斜角 φ は北傾斜を正とする。

水平面内の太陽の日射方向を x軸、鉛直上向きを z軸とする。
パネルの北端のある点を点Pとし、点P の鉛直線が大地と交わる点を原点 O とする。
点P が隣りのパネルに影を落とさない条件を計算する。

計算

点P の大地からの高さ h は、次式となる。h は北傾斜 φ > 0 で大きく、南傾斜 φ < 0 で小さくなる。
h = L sin θ + L cos θ tan φ 　　式1

x-z軸平面で、点P をかすめる太陽光の直線の式は次式となる。
z = h - x tan α 　　式2

x-z軸平面で大地の直線の式は、x軸が南北軸から β だけ傾いていることを考慮すると次式となる。
z = - x tan φ cos β 　　式3

式2、式3から、x軸上で点P をかすめる太陽光と大地との交点から原点O までの距離 d_x は次式となる。
d_x = h / ( tan α - tan φ cos β )
= L × ( sin θ + cos θ tan φ ) / ( tan α - tan φ cos β ) 　　式4

距離 d_x は x軸に投影された距離なので、南北軸上の距離 d に変換すると次式となる。
d = d_x cos β
= L × cos β ( sin θ + cos θ tan φ ) / ( tan α - tan φ cos β )　　式5

式5 は点P が大地に作る影の南北方向の距離である。よって、隣のパネルに影を落とさないために必要な列間の最小距離でもある。

計算例

緯度 35 °、パネル長 L = 10 m 、冬至の南中時に影ができない条件の計算例である。
冬至の南中時なので、太陽高度 α = 90 - 23.4 - 35 = 31.6 °、太陽方位 β = 0°である。
パネルの傾斜が大きくなるほど、影ができないための距離は増加する。
パネルの傾斜と地面の傾斜が同じ場合は、平行になるので必要な距離は 0 になる。
北傾斜では影ができないための距離は南傾斜より増加する。

地面の傾斜		パネルの傾斜 (南向き)
		5°	10°	15°	20°	25°	30°
南傾斜	-30°	-4.09	-3.31	-2.51	-1.68	-0.84	0
	-25°	-3.49	-2.64	-1.77	-0.89	0	0.89
	-20°	-2.81	-1.89	-0.95	0	0.95	1.89
	-15°	-2.04	-1.02	0	1.02	2.04	3.03
	-10°	-1.12	0	1.12	2.23	3.32	4.39
	-5°	0	1.25	2.48	3.70	4.89	6.04
水平	0°	1.42	2.82	4.21	5.56	6.87	8.13
北傾斜	5°	3.30	4.92	6.51	8.04	9.51	10.91
	10°	5.99	7.91	9.78	11.57	13.27	14.87
	15°	10.20	12.60	14.91	17.10	19.16	21.08
	20°	17.90	21.18	24.30	27.23	29.95	32.45
	25°	37.05	42.50	47.63	52.40	56.77	60.70
	30°	174.96	196.08	215.70	233.68	249.88	264.17