多人数 n人から一人の勝者を決めるじゃんけんの平均回数
多人数 (n人とする) から一人の勝者を決めるじゃんけんの回数の期待値を計算する。
じゃんけんの回数は、あいこを含む回数 NA(n) と あいこを含まない回数 NB(n) を求める。
n 人じゃんけんを1回だけ実行した時にあいこになる確率を Pd(n) とする ( d は英語の draw より)。
参加者はグーチョキパーを等確率 1/3 で出すものとする。
二人 (n=2) の場合
| 2人目 \ 1人目 | グー | チョキ | パー |
|---|---|---|---|
| グー | あいこ | 終了 | 終了 |
| チョキ | 終了 | あいこ | 終了 |
| パー | 終了 | 終了 | あいこ |
二人の場合は勝負がつけばおしまいなので、あいこを含まない回数の期待値は NB(2)=1 である。
表より、じゃんけんを1回だけした時にあいこになる確率は Pd(2) = 3/9 = 1/3 である。
あいこを含む回数の期待値 NA(2) を計算する。
i 回で勝負がつくのは、(i-1)回あいこが続いた後 勝敗が決まる場合なので、その確率は (1 - Pd(2))・Pdi-1(2) である。
従って、勝負がつくまでの回数の期待値は次式となる。
NA(2) = 1・{ 1 - Pd(2) } + 2・Pd(2)・{ 1 - Pd(2) } + 3・Pd2(2)・{ 1 - Pd(2) } + … + i・Pdi-1(2)・{ 1 - Pd(2) } + …
= { 1 - Pd(2) } × { 1 + 2・Pd(2) + 3・Pd2(2) + … + i・Pdi-1(2) + … }
この式を変形と等比級数の和の公式で計算すると、
NA(2) = 1 / { 1 - Pd(2) } = 1 / { 1 - 1/3 } = 3/2 = 1.5
三人 (n=3) の場合
| 1人目 | グー | チョキ | パー | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 3人目 \ 2人目 | グー | チョキ | パー | グー | チョキ | パー | グー | チョキ | パー |
| グー | あいこ | 2人勝 | 1人勝 | 2人勝 | 1人勝 | あいこ | 1人勝 | あいこ | 2人勝 |
| チョキ | 2人勝 | 1人勝 | あいこ | 1人勝 | あいこ | 2人勝 | あいこ | 2人勝 | 1人勝 |
| パー | 1人勝 | あいこ | 2人勝 | あいこ | 2人勝 | 1人勝 | 2人勝 | 1人勝 | あいこ |
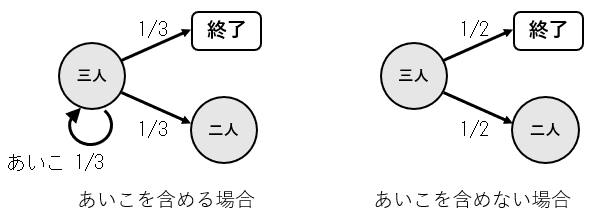
最初に、あいこを含む回数の期待値 NA(3) を計算する。
三人ジャンケンの場合は 1回ジャンケンを行うと、 1/3の確率で一人勝ちで終了、1/3の確率であいこ、1/3の確率で二人勝ちになる。
あいこの場合は引き続き三人じゃけんを行い、二人勝ちの場合は二人ジャンケンに移行する。よって NA(3) は、
NA(3) = (1/3)・1 + (1/3)・{ NA(3) + 1} + (1/3)・{ NA(2) + 1}
これを解くと、
NA(3) = 9/4 = 2.25
次に、あいこを含まない回数の期待値 NB(3) を計算する。
あいこをカウントしない場合は、1/2の確率で一人勝ちで終了、1/2の確率で二人勝ちで二人ジャンケンに移行する。よって NB(3) は、
NB(3) = (1/2)・1 + (1/2)・{ NB(2) + 1} = 1/2 + 2/2 = 3/2 = 1.5
一般化 n人の場合
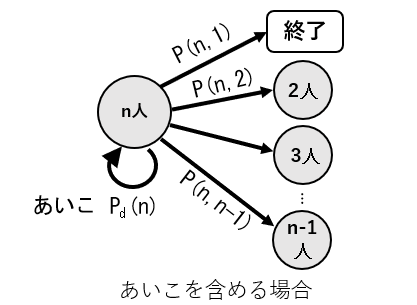
最初に、あいこを含む回数の期待値 NA(n) について考える。
1回のn人ジャンケンで、勝者が i 人となる確率を P(n, i) として、これを計算する。
n人から i 人の勝者を選ぶ組み合わせは、nCi 個ある。
勝者が出す手の種類は、グーチョキパーの3種類がある。勝者の手が決まれば敗者の手は必然的に決まる。
よって、n人から i 人の勝者が生まれるジャンケンの出し方の組み合わせは、3 × nCi となる。
n人が出す可能性がある全ての手の組み合わせは、3n なので、P(n, i) は次式となる。
P(n, i) = 3 × nCi / 3n = nCi / 3n-1
あいこが発生する確率 Pd(n) は、勝敗がついた場合の余事象なので
Pd(n) = 1 - { P(n, 1) + P(n, 2) + P(n, 3) + … + P(n, n-1) }
1回ジャンケンを行うと、 P(n, 1) の確率で一人勝ちで終了、Pd(n) の確率であいこ、P(n, i) の確率で i人勝ち(i=2...n-1) になる。
あいこの場合は引き続きじゃけんを行い、i人勝ちの場合は i人ジャンケンに移行する。よって NA(n) は、
NA(n) = P(n, 1)・1 + Pd(n)・{ NA(n) + 1} + Σi=2...n-1 P(n, i)・{ NA(i) + 1}
これを整理すると次の漸化式が得られる。
NA(n) = { 1 + Σi=2...n-1 P(n, i)・NA(i) } / Σi=1...n-1 P(n, i)

次に、あいこを含まない回数の期待値 NB(n) について考える。
n人じゃけんで勝敗が決まった場合について、i人勝ちの確率を Q(n, i) とする。
Q(n, i) = P(n, i) / P(あいこ以外の全て) = P(n, i) / Σi=1...n-1 P(n, i)
あいこを含まない場合は、Q(n, 1) の確率で一人勝ちで終了、Q(n, i) の確率で i人勝ち(i=2...n-1) で i人ジャンケンに移行する。よって NB(n) は、
NB(n) = Q(n, 1)・1 + Σi=2...n-1 Q(n, i)・{ NB(i) + 1}
これを整理すると次の漸化式が得られる。
NB(n) = 1 + Σi=2...n-1 Q(n, i)・NB(i)
数値計算例
n=100 まで計算したものが下の表である。nが大きくなると、あいこを含む回数の期待値 NA(n) は急激に増加する。
仮に1回のジャンケンにかかる時間が 4秒とすると、1分で終わらせたいならば 8人くらいが限度である。
| 人数 n | あいこを含む回数の期待値 NA(n) | あいこを含まない回数の期待値 NB(n) |
|---|---|---|
| 2 | 1.5 | 1 |
| 3 | 2.25 | 1.5 |
| 4 | 3.2142857142857 | 1.8571428571429 |
| 5 | 4.4857142857143 | 2.1428571428571 |
| 6 | 6.2198156682028 | 2.3824884792627 |
| 7 | 8.6467357910906 | 2.5887096774194 |
| 8 | 12.104443799364 | 2.7693675387351 |
| 9 | 17.09193529177 | 2.9298958597917 |
| 10 | 24.349597758456 | 3.0742546377461 |
| 11 | 34.979460986691 | 3.2053996730303 |
| 12 | 50.625020516755 | 3.3255704967707 |
| 13 | 73.740353108861 | 3.4364874605658 |
| 14 | 107.99313367331 | 3.5394920558707 |
| 15 | 158.86844072976 | 3.6356474966119 |
| 16 | 234.57363419553 | 3.7258106160269 |
| 17 | 347.39467747336 | 3.8106831374111 |
| 18 | 515.7294029045 | 3.8908483027338 |
| 19 | 767.13590259811 | 3.966797225165 |
| 20 | 1142.903239255 | 4.0389480770663 |
| 21 | 1704.9051738955 | 4.1076602867636 |
| 22 | 2545.8778387886 | 4.1732452404424 |
| 23 | 3804.83260261 | 4.2359745109028 |
| 24 | 5690.1708170716 | 4.2960863091721 |
| 25 | 8514.350252507 | 4.3537906346529 |
| 26 | 12745.87765078 | 4.4092734517715 |
| 27 | 19087.288684592 | 4.4627001224069 |
| 28 | 28592.106815003 | 4.5142182573551 |
| 29 | 42840.267732734 | 4.5639601056204 |
| 30 | 64201.238721485 | 4.6120445700322 |
| 31 | 96228.676088044 | 4.658578916703 |
| 32 | 144252.38429832 | 4.7036602310051 |
| 33 | 216266.22093044 | 4.7473766619902 |
| 34 | 324259.91192755 | 4.7898084891768 |
| 35 | 486216.72176909 | 4.8310290395261 |
| 36 | 729109.89285762 | 4.8711054776547 |
| 37 | 1093397.2222779 | 4.9100994885181 |
| 38 | 1639762.824053 | 4.9480678687047 |
| 39 | 2459229.6439456 | 4.9850630399272 |
| 40 | 3688328.070956 | 5.0211334961823 |
| 41 | 5531848.6537142 | 5.0563241942702 |
| 42 | 8296970.9240296 | 5.0906768958768 |
| 43 | 12444456.318452 | 5.1242304681598 |
| 44 | 18665437.168444 | 5.1570211487187 |
| 45 | 27996599.695473 | 5.1890827799303 |
| 46 | 41992957.890985 | 5.2204470168719 |
| 47 | 62987013.570589 | 5.2511435124138 |
| 48 | 94477495.498185 | 5.2812000825226 |
| 49 | 141712466.87576 | 5.3106428543581 |
| 50 | 212563985.08269 | 5.3394963993655 |
| 51 | 318840089.41555 | 5.3677838532353 |
| 52 | 478252780.3614 | 5.3955270243343 |
| 53 | 717369985.58748 | 5.4227464919794 |
| 54 | 1076043505.2753 | 5.4494616957292 |
| 55 | 1614050925.5593 | 5.4756910167083 |
| 56 | 2421058482.9811 | 5.5014518518391 |
| 57 | 3631565354.0424 | 5.5267606817372 |
| 58 | 5447320080.6234 | 5.5516331329316 |
| 59 | 8170945196.9712 | 5.5760840349824 |
| 60 | 12256374156.261 | 5.6001274730007 |
| 61 | 18384506703.031 | 5.6237768360111 |
| 62 | 27576691910.089 | 5.6470448615501 |
| 63 | 41364952706.67 | 5.6699436768428 |
| 64 | 62047322636.688 | 5.6924848368665 |
| 65 | 93070850953.634 | 5.7146793595755 |
| 66 | 139606110209.8 | 5.7365377585305 |
| 67 | 209408957573.74 | 5.7580700731546 |
| 68 | 314113176723.5 | 5.7792858968121 |
| 69 | 471169440582.69 | 5.8001944028898 |
| 70 | 706753755295 | 5.820804369043 |
| 71 | 1060130126023.9 | 5.8411241997516 |
| 72 | 1590194555449.5 | 5.8611619473214 |
| 73 | 2385291041260.7 | 5.8809253314512 |
| 74 | 3577935572077.1 | 5.9004217574772 |
| 75 | 5366902120935.8 | 5.9196583333952 |
| 76 | 8050351635027.1 | 5.9386418857554 |
| 77 | 12075525519680 | 5.957378974512 |
| 78 | 18113285863569 | 5.9758759069092 |
| 79 | 27169925775553 | 5.9941387504715 |
| 80 | 40754884888736 | 6.0121733451675 |
| 81 | 61132322615037 | 6.0299853148058 |
| 82 | 91698478025168 | 6.0475800777194 |
| 83 | 1.3754770966624E+14 | 6.0649628567903 |
| 84 | 2.0632155528523E+14 | 6.0821386888608 |
| 85 | 3.0948232141044E+14 | 6.0991124335764 |
| 86 | 4.6422346771924E+14 | 6.1158887816995 |
| 87 | 6.9633518358368E+14 | 6.1324722629311 |
| 88 | 1.044502752882E+15 | 6.1488672532762 |
| 89 | 1.5667541012064E+15 | 6.1650779819825 |
| 90 | 2.3501311166645E+15 | 6.1811085380827 |
| 91 | 3.5251966310658E+15 | 6.1969628765688 |
| 92 | 5.2877948916858E+15 | 6.21264482422 |
| 93 | 7.9316922688882E+15 | 6.228158085111 |
| 94 | 1.1897538317532E+16 | 6.2435062458195 |
| 95 | 1.784630736905E+16 | 6.2586927803541 |
| 96 | 2.6769460919515E+16 | 6.2737210548198 |
| 97 | 4.0154191211698E+16 | 6.2885943318392 |
| 98 | 6.0231286608081E+16 | 6.3033157747445 |
| 99 | 9.0346929650291E+16 | 6.3178884515542 |
| 100 | 1.3552039414815E+17 | 6.3323153387498 |