緯度・経度で表現された 2点間の距離の中間点の計算方法
緯度・経度で表現された 2点間の距離の中間点を求める計算式を導出する。
地球を球と仮定し、地球の中心を原点 O とする。
一方の点を P1、もう一方を P2 とする。角度の単位は rad である。
座標系
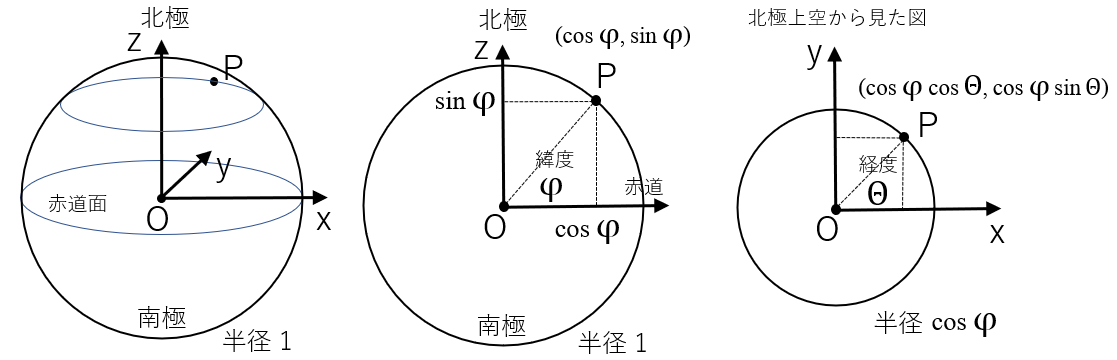
下図のような直交座標系を導入する。赤道面がx-y平面、自転軸がz軸である。
計算
この座標上で原点 O を中心とする半径 1 の球を考える。
球上の点Pの緯度を φ, 経度を θ とすると、直交座標は (x, y, z) = (cos φ cos θ , cos φ sin θ , sin φ) となる。
P1の緯度を φ1, 経度を θ1 とすると、直交座標は v1 = (x1, y1, z1) = (cos φ1 cos θ1 , cos φ1 sin θ1 , sin φ1) となる。
P2の緯度を φ2, 経度を θ2 とすると、直交座標は v2 = (x2, y2, z2) = (cos φ2 cos θ2 , cos φ2 sin θ2 , sin φ2) となる。
点P1 と P2 の直線上の中間点は、
vc = (xc , yc , zc) = (v1 + v2) × 0.5 = (x1 + x2 , y1 + y2 , z1 + z2) × 0.5
だが、これは地球の内側 (地中) である。地表上の位置になるように長さ 1 のベクトルに正規化すると、
vnc = (xnc , ync , znc) = vc / |vc| = (xc , yc , zc) / √(xc2+yc2+zc2)
上式は直交座標系なので、緯度 φc、経度 θc に変換する。
xnc = cos φc cos θc
ync = cos φc sin θc
znc = sin φc
を解くと、
φc = arcsin(znc)
θc = arctan2(ync , xnc) ※ 引数を 2個取り、象限の場合分けをしてくれる arctan関数
数値計算に使用するにはこれで構わないが、残念ながらあまり見通しの良い式ではない。
補足
説明の都合で、vc の計算で 0.5 を掛けたが、vn で正規化するので掛ける必要はない。
2点が対蹠点 (地球の真反対) の時は、vc = (0, 0, 0) となり、正規化の際に 0割りが発生するので必要に応じて判定する。
計算機
数値を入力してエンターを押してください。西経、南緯はマイナスで入力してください。
| 緯度 | 経度 | |
|---|---|---|
| P1 | ||
| P2 | ||
| 中間点 |