緯度・経度で表現された 2点間の距離の計算方法
地球を球と仮定した場合の、緯度・経度で表現された 2点間の距離の計算式を導出する。
地球の半径を R = 40000 / 2π = 6366 km とする。
地球の中心を原点 O、計測したい点の一方を P1、もう一方を P2 とする。角度の単位は rad である。
成す角が分かれば2点間の距離は分かる
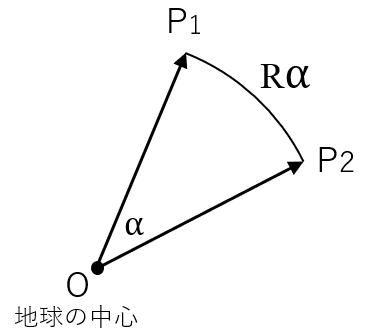
地球上の2点間の距離は、2点と地球の中心を通る平面上の円弧の長さである。
円弧の長さは、円の半径と、地球の中心 O から P1 と O から P2 の成す角 α から計算できる。
地球の半径は既知なので、成す角を求めればよい。
成す角 α を求めるため内積を計算する
長さ1 同士のベクトルの内積は cos α となる。よって単位ベクトルの内積を計算すれば α が求まる。
内積を計算するため、下図のような直交座標系を導入する。赤道面がx-y平面、自転軸がz軸である。
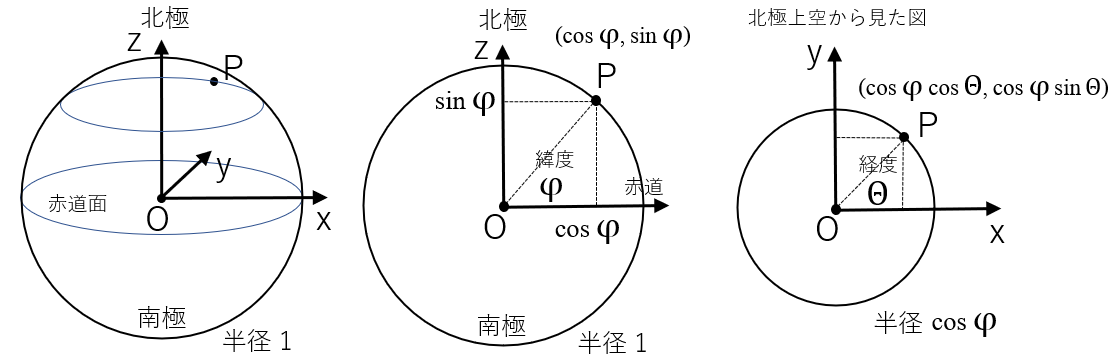
この座標上で原点 O を中心とする半径 1 の球を考える。
球上の点Pの緯度を φ, 経度を θ とすると、直交座標は (x, y, z) = (cos φ cos θ , cos φ sin θ , sin φ) となる。
P1の緯度を φ1, 経度を θ1 とすると、直交座標は v1 = (cos φ1 cos θ1 , cos φ1 sin θ1 , sin φ1) となる。
P2の緯度を φ2, 経度を θ2 とすると、直交座標は v2 = (cos φ2 cos θ2 , cos φ2 sin θ2 , sin φ2) となる。
v1とv2の内積を計算すると、
v1・v2 = cos α = cos φ1 cos θ1 cos φ2 cos θ2 + cos φ1 sin θ1 cos φ2 sin θ2 + sin φ1 sin φ2
よって成す角 α は、
α = arccos (cos φ1 cos θ1 cos φ2 cos θ2 + cos φ1 sin θ1 cos φ2 sin θ2 + sin φ1 sin φ2)
ただし、arccosは 0~π の範囲で値を返すものとする。距離 L は、
L = R α = R × arccos (cos φ1 cos θ1 cos φ2 cos θ2 + cos φ1 sin θ1 cos φ2 sin θ2 + sin φ1 sin φ2)
検算
成す角 α が自明な場合について、導出した式を検算してみる。
2点が同一地点の場合
2点が同一地点の場合、すなわち φ1 = φ2 , θ1 = θ2の場合、
α = arccos (cos φ1 cos θ1 cos φ1 cos θ1 + cos φ1 sin θ1 cos φ1 sin θ1 + sin φ1 sin φ1)
= arccos (cos2 φ1 cos2 θ1 + cos2 φ1 sin2 θ1 + sin2 φ1)
= arccos (cos2 φ1 + sin2 φ1) = arccos 1 = 0
赤道上の2点の場合
2点が赤道上の場合、すなわち φ1 = φ2 = 0 の場合、
α = arccos (cos 0 cos θ1 cos 0 cos θ2 + cos 0 sin θ1 cos 0 sin θ2 + sin 0 sin 0)
= arccos (cos θ1 cos θ2 + sin θ1 sin θ2) = arccos {cos(θ1 - θ2)} = |θ1 - θ2|
同一子午線上の2点の場合
2点が同一子午線上の場合、すなわち θ1 = θ2 の場合、
α = arccos (cos φ1 cos θ1 cos φ2 cos θ1 + cos φ1 sin θ1 cos φ2 sin θ1 + sin φ1 sin φ2)
= arccos (cos φ1 cos φ2 cos2 θ1 + cos φ1 cos φ2 sin2 θ1 + sin φ1 sin φ2)
= arccos (cos φ1 cos φ2 + sin φ1 sin φ2) = arccos {cos(φ1 - φ2)} = |φ1 - φ2|
問題なさそうである。