すごろくでサイコロを何回振ればゴールできるか? サイコロが2個の場合
以前、サイコロを1個使うのすごろく(ゴールでの跳ね返りあり)に関して、ゴールまでにサイコロを振る回数の期待値(平均)を求めた。
今回はサイコロを 2個用いて和の数だけ進む場合について、ゴールまでにサイコロを振る回数の期待値(平均)を計算する。
すごろくのルールなどは前回に準ずる。
サイコロが 1個の場合と 2個の場合で違うのは、出る目(の和)の確率分布である。
1個の場合は 1~6 まで等確率だが、2個の場合は 2~12 のうち 7の組み合わせ (1,6), (2,5), (3,4), (4,3), (5,2), (6,1) が最も発生しやすい。
12マスのすごろく
最初に12マス(ゴールを含まない)のすごろくについて、各マスからゴールするまでの回数を考える。
マスを、ゴールから近い順に q1, q2, …, q12 とする。
マス qi から ゴールに到達するまでにサイコロを振る平均回数を xi とする。
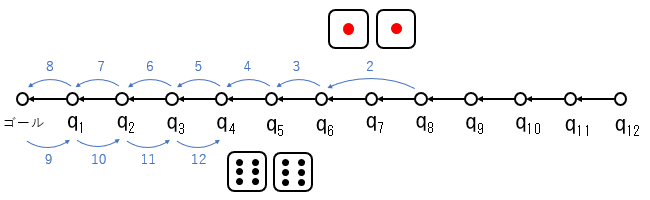
例として、q8 からスタートする場合を考える。
和 8 がでれば、ゴールである。組み合わせは (2,6),(3,5),(4,4),(5,3),(6,2)、確率は 5/36、ゴールまでの回数は 1 である。
和 2 がでれば、q6 に移動する。組み合わせは (1,1)、確率は 1/36、ゴールまでの平均回数は 1 + x6 である。
和 3 がでれば、q5 に移動する。組み合わせは (1,2),(2,1)、確率は 2/36、ゴールまでの平均回数は 1 + x5 である。
和 4 又は 12 がでれば、q4 に移動する。組み合わせは (1,3),(2,2),(3,1),(6,6)、確率は 4/36、ゴールまでの平均回数は 1 + x4 である。
和 5 又は 11 がでれば、q3 に移動する。組み合わせは (1,4),(2,3),(3,2),(4,1),(5,6),(6,5)、確率は 6/36、ゴールまでの平均回数は 1 + x3 である。
和 6 又は 10 がでれば、q2 に移動する。組み合わせは (1,5),(2,4),(3,3),(4,2),(5,1),(4,6),(5,5),(6,4)、確率は 8/36、ゴールまでの平均回数は 1 + x2 である。
和 7 又は 9 がでれば、q1 に移動する。組み合わせは (1,6),(2,5),(3,4),(4,3),(5,2),(6,1),(3,6),(4,5),(5,4),(6,3)、確率は 10/36、ゴールまでの平均回数は 1 + x1 である。
よって、q8 から ゴールに到達するまでにサイコロを振る回数の期待値 x8 は、次式となる。
x 8 = (1 / 36) × { 5 + 10(1 + x1) + 8(1 + x2) + 6(1 + x3) + 4(1 + x4) + 2(1 + x5) + 1(1 + x6) }
同様に立式すると、12個の未知数に対して 12個の式ができる。
x 1 = (1 / 36) × { 0 + 1(1 + x1) + 2(1 + x2) + 3(1 + x3) + 4(1 + x4) + 5(1 + x5) + 6(1 + x6) + 5(1 + x7) + 4(1 + x8) + 3(1 + x9) + 2(1 + x10) + 1(1 + x11) }
x 2 = (1 / 36) × { 1 + 2(1 + x1) + 3(1 + x2) + 4(1 + x3) + 5(1 + x4) + 6(1 + x5) + 5(1 + x6) + 4(1 + x7) + 3(1 + x8) + 2(1 + x9) + 1(1 + x10) }
x 3 = (1 / 36) × { 2 + 4(1 + x1) + 4(1 + x2) + 5(1 + x3) + 6(1 + x4) + 5(1 + x5) + 4(1 + x6) + 3(1 + x7) + 2(1 + x8) + 1(1 + x9) }
x 4 = (1 / 36) × { 3 + 6(1 + x1) + 6(1 + x2) + 6(1 + x3) + 5(1 + x4) + 4(1 + x5) + 3(1 + x6) + 2(1 + x7) + 1(1 + x8) }
x 5 = (1 / 36) × { 4 + 8(1 + x1) + 8(1 + x2) + 6(1 + x3) + 4(1 + x4) + 3(1 + x5) + 2(1 + x6) + 1(1 + x7) }
x 6 = (1 / 36) × { 5 + 10(1 + x1) + 8(1 + x2) + 6(1 + x3) + 4(1 + x4) + 2(1 + x5) + 1(1 + x6) }
x 7 = (1 / 36) × { 6 + 10(1 + x1) + 8(1 + x2) + 6(1 + x3) + 4(1 + x4) + 2(1 + x5) }
x 8 = (1 / 36) × { 5 + 10(1 + x1) + 8(1 + x2) + 6(1 + x3) + 4(1 + x4) + 2(1 + x5) + 1(1 + x6) }
x 9 = (1 / 36) × { 4 + 8(1 + x1) + 8(1 + x2) + 6(1 + x3) + 4(1 + x4) + 3(1 + x5) + 2(1 + x6) + 1(1 + x7) }
x10 = (1 / 36) × { 3 + 6(1 + x1) + 6(1 + x2) + 6(1 + x3) + 5(1 + x4) + 4(1 + x5) + 3(1 + x6) + 2(1 + x7) + 1(1 + x8) }
x11 = (1 / 36) × { 2 + 4(1 + x1) + 4(1 + x2) + 5(1 + x3) + 6(1 + x4) + 5(1 + x5) + 4(1 + x6) + 3(1 + x7) + 2(1 + x8) + 1(1 + x9) }
x12 = (1 / 36) × { 1 + 2(1 + x1) + 3(1 + x2) + 4(1 + x3) + 5(1 + x4) + 6(1 + x5) + 5(1 + x6) + 4(1 + x7) + 3(1 + x8) + 2(1 + x9) + 1(1 + x10) }
これを解くのはかなり面倒だが、解くと次のようになる。
| 位置 | ゴールまでにサイコロを振る回数の期待値 xi |
| q1 | 5276734 / 375695 = 14.04526 (最大) |
| q2 | 5170824 / 375695 = 13.76336 |
| q3 | 5080174 / 375695 = 13.52207 |
| q4 | 4994424 / 375695 = 13.29383 |
| q5 | 4903774 / 375695 = 13.05254 |
| q6 | 4797864 / 375695 = 12.77064 |
| q7 | 4664590 / 375695 = 12.4159 (最小) |
| q8 | 4797864 / 375695 = 12.77064 |
| q9 | 4903774 / 375695 = 13.05254 |
| q10 | 4994424 / 375695 = 13.29383 |
| q11 | 5080174 / 375695 = 13.52207 |
| q12 | 5170824 / 375695 = 13.76336 |
この表によるとサイコロが 1個の場合と異なり、位置により優劣がある。q7 が一番小さく有利である。
ゴール直前の q1 が一番大きいのは、どの目の組み合わせが出ても 1回ではゴールできないからだろう。
またサイコロが 1個の場合は平均回数が 6であるのに対して、2個の場合は 12~14 程度で約2倍である。
サイコロが 2個の場合は 1個の場合よりゴールしにくく、ゴール付近で滞留しやすいことがわかる。
nマスのすごろく
次に一般化して nマス(ゴールを含まない, n ≧ 12) のすごろくについて、スタートからゴールするまでにサイコロを振る回数の期待値 xn を計算する。
先ほど求めた xi (i ≦ 12) は、12マスのすごろくで位置 qi から開始した時にゴールに達するまでにサイコロを振る回数の期待値だが、
これから求める xi (i ≧ 12) は、iマスのすごろくでスタートから開始した時にゴールに達するまでにサイコロを振る回数の期待値である。
意味が異なるので注意する。x12 は両方の意味を含んでいる。
n > 12 の場合には、1回でゴールする可能性はない。
1回目の番に qn から 2 ~ 12 マス前方のマス、すなわち qn-2 ~ qn-12 に移動する。
よって xn-2 ~ xn-12 が分かっているとすると、サイコロの目の和の確率分布を考慮して xn は漸化式で次のようにかける。
xn = 1 + ( 1xn-2 + 2xn-3 + 3xn-4 + 4xn-5 + 5xn-6 + 6xn-7 + 5xn-8 + 4xn-9 + 3xn-10 + 2xn-11 + 1xn-12) / 36
下の表は、100マスの場合まで計算した期待値である。比較用にサイコロが 1個の場合も併記した。
マスの数が 50 以下の場合にはサイコロが1個の方が少ない回数で、51 以上の場合には2個の方が少ない回数でゴールできることがわかる。
| すごろくのマスの数 n (ゴールを含まない) | ゴールまでにサイコロを振る回数の期待値 xn | ||
| サイコロが 1個の場合 | サイコロが 2個の場合 | ||
| 12 | 8.161 | 13.763 | |
| 13 | 8.522 | 14.045 | |
| 14 | 8.775 | 14 | |
| 15 | 9.043 | 14.045 | |
| 16 | 9.324 | 14.152 | |
| 17 | 9.613 | 14.3 | |
| 18 | 9.906 | 14.471 | |
| 19 | 10.197 | 14.651 | |
| 20 | 10.476 | 14.823 | |
| 21 | 10.76 | 14.967 | |
| 22 | 11.046 | 15.099 | |
| 23 | 11.333 | 15.23 | |
| 24 | 11.62 | 15.363 | |
| 25 | 11.905 | 15.5 | |
| 26 | 12.19 | 15.642 | |
| 27 | 12.476 | 15.791 | |
| 28 | 12.762 | 15.94 | |
| 29 | 13.048 | 16.086 | |
| 30 | 13.333 | 16.229 | |
| 31 | 13.619 | 16.37 | |
| 32 | 13.905 | 16.511 | |
| 33 | 14.19 | 16.652 | |
| 34 | 14.476 | 16.794 | |
| 35 | 14.762 | 16.938 | |
| 36 | 15.048 | 17.081 | |
| 37 | 15.333 | 17.225 | |
| 38 | 15.619 | 17.368 | |
| 39 | 15.905 | 17.511 | |
| 40 | 16.19 | 17.654 | |
| 41 | 16.476 | 17.796 | |
| 42 | 16.762 | 17.939 | |
| 43 | 17.048 | 18.081 | |
| 44 | 17.333 | 18.224 | |
| 45 | 17.619 | 18.367 | |
| 46 | 17.905 | 18.51 | |
| 47 | 18.19 | 18.653 | |
| 48 | 18.476 | 18.796 | |
| 49 | 18.762 | 18.939 | |
| 50 | 19.048 | 19.082 | |
| 51 | 19.333 | 19.225 | |
| 52 | 19.619 | 19.367 | |
| 53 | 19.905 | 19.51 | |
| 54 | 20.19 | 19.653 | |
| 55 | 20.476 | 19.796 | |
| 56 | 20.762 | 19.939 | |
| 57 | 21.048 | 20.082 | |
| 58 | 21.333 | 20.225 | |
| 59 | 21.619 | 20.367 | |
| 60 | 21.905 | 20.51 | |
| 61 | 22.19 | 20.653 | |
| 62 | 22.476 | 20.796 | |
| 63 | 22.762 | 20.939 | |
| 64 | 23.048 | 21.082 | |
| 65 | 23.333 | 21.225 | |
| 66 | 23.619 | 21.367 | |
| 67 | 23.905 | 21.51 | |
| 68 | 24.19 | 21.653 | |
| 69 | 24.476 | 21.796 | |
| 70 | 24.762 | 21.939 | |
| 71 | 25.048 | 22.082 | |
| 72 | 25.333 | 22.225 | |
| 73 | 25.619 | 22.367 | |
| 74 | 25.905 | 22.51 | |
| 75 | 26.19 | 22.653 | |
| 76 | 26.476 | 22.796 | |
| 77 | 26.762 | 22.939 | |
| 78 | 27.048 | 23.082 | |
| 79 | 27.333 | 23.225 | |
| 80 | 27.619 | 23.367 | |
| 81 | 27.905 | 23.51 | |
| 82 | 28.19 | 23.653 | |
| 83 | 28.476 | 23.796 | |
| 84 | 28.762 | 23.939 | |
| 85 | 29.048 | 24.082 | |
| 86 | 29.333 | 24.225 | |
| 87 | 29.619 | 24.367 | |
| 88 | 29.905 | 24.51 | |
| 89 | 30.19 | 24.653 | |
| 90 | 30.476 | 24.796 | |
| 91 | 30.762 | 24.939 | |
| 92 | 31.048 | 25.082 | |
| 93 | 31.333 | 25.225 | |
| 94 | 31.619 | 25.367 | |
| 95 | 31.905 | 25.51 | |
| 96 | 32.19 | 25.653 | |
| 97 | 32.476 | 25.796 | |
| 98 | 32.762 | 25.939 | |
| 99 | 33.048 | 26.082 | |
| 100 | 33.333 | 26.225 | |