Top　　関連リンク [続・すごろくでサイコロを何回振ればゴールできるか? 分散・標準偏差]　,　[サイコロが2個の場合]

---

すごろくでサイコロを何回振ればゴールできるか?　マス数とターン数の関係

わたてんを見ていたら、ひなた達がすごろくを作っていた。それでふと考えた。
すごろくのマス数が分かっている場合、サイコロを平均何回振ればゴールできるのだろうか。
または逆に、ゴールまでにサイコロを振る平均回数をある値にしたい場合、すごろくは何マスにすればよいのだろうか。

ルールと仮定

ローカルルールがあるかもしれないので、ここで考えるすごろくのルールを明確にしておく。

・進むマス目に他者のコマがあった場合でも、影響はないものとする。
・ゴールするには、ちょうどの目を出さなければならない。ゴールまでのマス数に対して多すぎる目が出た場合は、ゴールから逆方向に超過分だけ戻ることとする。

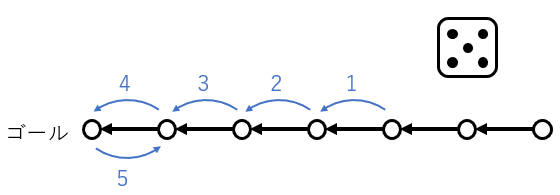
1番目のルールより、他者の干渉がないので自分の(一人分の)操作だけを計算すればよいことになる。
またルールではないが、計算の都合上 次の仮定を設ける。
・コースはスタートからゴールまで一直線である。分岐やループはない。
・1回休み・ジャンプ(振り出しに戻るなど) はない。
・使用するサイコロは 1個とする。

6マスのすごろく

最初に6マス(ゴールを含まない)しかない短いすごろくについて考える。
マスを、ゴールから近い順に q₁, q₂, q₃, q₄, q₅, q₆ とする。
マス q_i から ゴールに到達するまでにサイコロを振る平均回数を x_i とする。


例として、q₄ にいる場合を考える。
4 がでれば、ゴールである。確率は 1/6 で、ゴールまでの回数は 1 である。
1 がでれば、q₃ に移動する。確率は 1/6 で、ゴールまでの平均回数は 1 + x₃ である。
2・6 がでれば、q₂ に移動する。確率は 2/6 で、ゴールまでの平均回数は 1 + x₂ である。
3・5 がでれば、q₁ に移動する。確率は 2/6 で、ゴールまでの平均回数は 1 + x₁ である。
よって、q₄ から ゴールに到達するまでにサイコロを振る回数の期待値 x₄ は、次式となる。
x₄ = 1・1/6 + (1 + x₁)・2/6 + (1 + x₂)・2/6 + (1 + x₃)・1/6

同様に立式すると、6個の未知数に対して 6個の式ができる。

x₁ = 1・1/6 + (1 + x₁)・1/6 + (1 + x₂)・1/6 + (1 + x₃)・1/6 + (1 + x₄)・1/6 + (1 + x₅)・1/6
x₂ = 1・1/6 + (1 + x₁)・2/6 + (1 + x₂)・1/6 + (1 + x₃)・1/6 + (1 + x₄)・1/6
x₃ = 1・1/6 + (1 + x₁)・2/6 + (1 + x₂)・2/6 + (1 + x₃)・1/6
x₄ = 1・1/6 + (1 + x₁)・2/6 + (1 + x₂)・2/6 + (1 + x₃)・1/6
x₅ = 1・1/6 + (1 + x₁)・2/6 + (1 + x₂)・1/6 + (1 + x₃)・1/6 + (1 + x₄)・1/6
x₆ = 1・1/6 + (1 + x₁)・1/6 + (1 + x₂)・1/6 + (1 + x₃)・1/6 + (1 + x₄)・1/6 + (1 + x₅)・1/6

これを解くのは結構面倒だが(検算は容易)、解くと
x₁ = x₂ = x₃ = x₄ = x₅ = x₆ = 6
となる。つまりどの位置からでも等しく平均 6 回サイコロを振ることになる。
なんとこの短いすごろくの場合は、位置がどこでも優劣はないのである。
一般のもっと長いすごろくでも、終盤で最後の 6マス以内にメンバーが団子になっている場合は同じことがいえる。

別解

同じことを別の視点からも計算することができる。
6マスのすごろくの場合、どの位置でもある値が出ればゴールできる状態になっている(確率 1/6)。
出なければ、引き続きサイコロを振る状態に戻る(確率 5/6)。
つまり下図のような状態になっている。

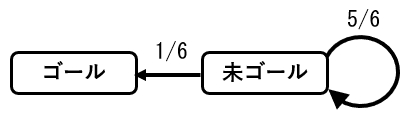
未ゴールを初期状態として、ゴールに到達するまで回数の期待値 x の式は次のようになる。
x = 1 × (1/6) + 2 × (1/6)・(5/6) + 3 × (1/6)・(5/6)² + 4 × (1/6)・(5/6)³ + …

この式を、変形や等比級数の和の式を使って解いても x = 6 が得られる。
こちらの方法の方が連立方程式を解くより楽だろう。

nマスのすごろく

次に1マス追加した、7マス(ゴールを含まない)のすごろくでスタートからゴールまでにサイコロを振る回数の期待値 x₇ を計算する。

この場合は 1回でゴールする可能性はなく、次のマスは 1/6 の確率で q₁ ～ q₆ のどれかである。
q₁ ～ q₆ からゴールに達するまでの回数の期待値は x₁ = x₂ = x₃ = x₄ = x₅ = x₆ = 6 と求まっているので、 x₇ は
x₇ = (1/6)(1 + x₁) + (1/6)(1 + x₂) + (1/6)(1 + x₃) + (1/6)(1 + x₄) + (1/6)(1 + x₅) + (1/6)(1 + x₆)
= 1 + ( x₆ + x₅ + x₄ + x₃ + x₂ + x₁ ) / 6 = 7

以降同様にして、漸化的に n マスの場合の、サイコロを振る回数の期待値を求めることができる。
x_n = 1 + ( x_n-1 + x_n-2 + x_n-3 + x_n-4 + x_n-5 + x_n-6 ) / 6

下の表は、100マスの場合まで計算したゴールまでにサイコロを振る回数の期待値である。
マス数 n が十分に大きい領域では、nが 1増えるごとに、サイコロを振る回数 x_n はサイコロの目の期待値の逆数 1/3.5 ずつ増加する。

※注釈　上の議論では、同じ x_i という変数を使っているが、x_i (i≦6) と x_i (i≧6) は変数の意味が異なる。
　x_i (i≦6) は、6マスのすごろくで位置 q_i から開始した時にゴールに達するまでにサイコロを振る回数の期待値だが、
　x_i (i≧6) は、iマスのすごろくでスタートから開始した時にゴールに達するまでにサイコロを振る回数の期待値である。
　x₆ は、両方とも包括している。同じ変数を用いたのは、変数を分けると漸化式が 1つで書けないからである。

続・すごろくでサイコロを何回振ればゴールできるか?　分散・標準偏差
サイコロが2個の場合

すごろくのマスの数 n (ゴールを含まない)	ゴールまでにサイコロを振る回数の期待値 xn
6	6
7	7
8	7.167
9	7.361
10	7.588
11	7.853
12	8.161
13	8.522
14	8.775
15	9.043
16	9.324
17	9.613
18	9.906
19	10.197
20	10.476
21	10.76
22	11.046
23	11.333
24	11.62
25	11.905
26	12.19
27	12.476
28	12.762
29	13.048
30	13.333
31	13.619
32	13.905
33	14.19
34	14.476
35	14.762
36	15.048
37	15.333
38	15.619
39	15.905
40	16.19
41	16.476
42	16.762
43	17.048
44	17.333
45	17.619
46	17.905
47	18.19
48	18.476
49	18.762
50	19.048
51	19.333
52	19.619
53	19.905
54	20.19
55	20.476
56	20.762
57	21.048
58	21.333
59	21.619
60	21.905
61	22.19
62	22.476
63	22.762
64	23.048
65	23.333
66	23.619
67	23.905
68	24.19
69	24.476
70	24.762
71	25.048
72	25.333
73	25.619
74	25.905
75	26.19
76	26.476
77	26.762
78	27.048
79	27.333
80	27.619
81	27.905
82	28.19
83	28.476
84	28.762
85	29.048
86	29.333
87	29.619
88	29.905
89	30.19
90	30.476
91	30.762
92	31.048
93	31.333
94	31.619
95	31.905
96	32.19
97	32.476
98	32.762
99	33.048
100	33.333