関連リンク すごろくでサイコロを何回振ればゴールできるか? マス数とターン数の関係
関連リンク サイコロの目の和がある値になるパターンを数え上げる
サイコロの目の平均、分散、標準偏差
i 個目のサイコロの目を確率変数 xi とする。確率変数 x の期待値を E[x] とする。
目次
サイコロが1個の場合
サイコロを複数個 (または複数回) 振った場合の目の和
サイコロを複数個 (または複数回) 振った場合の目の積
サイコロが1個の場合
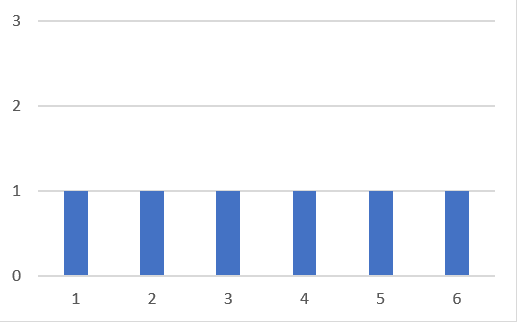
平均
μ = E[ x1 ] = (1/6) × (1 + 2 + 3 + 4 + 5 + 6) = 7/2
準備
E[ x12 ] = (1/6) × (12 + 22 + 32 + 42 + 52 + 62) = 91/6
分散
V = E[ x12 ] - E[ x1 ]2 = 91/6 - (7/2)2 = 35/12
標準偏差 σ = √V = √(35/12)
サイコロを複数個 (または複数回) 振った場合の目の和
サイコロが2個の場合の和
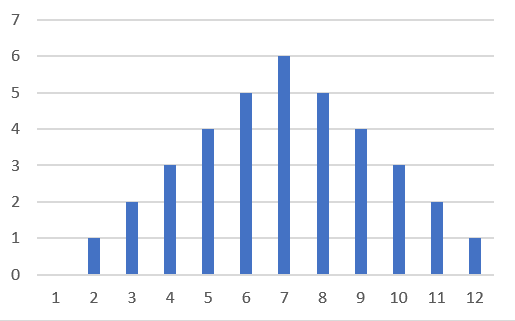
平均
μ2+ = E[ x1 + x2 ] = E[ x1 ] + E[ x2 ] = 2 E[ x1 ] = 2 × (7/2) = 7
準備
E[ x1x2 ] = (1/36) × Σi=1~6 { Σj=1~6 ( i × j ) }
= (1/36) × Σi { i × Σj j }
= (1/36) × Σi { 21・i }
= (1/36) × 21 × 21 = 49/4
E[ (x1 + x2)2 ] = E[ x12 ] + 2 E[ x1x2 ] + E[ x22 ]
= 2 E[ x12 ] + 2 E[ x1x2 ]
= 2・(91/6) + 2・(49/4) = 329/6
分散
V2+ = E[ (x1 + x2)2 ] - E[ x1 + x2 ]2 = 329/6 - 72 = 35/6
標準偏差 σ2+ = √V2+ = √(35/6)
一般化 サイコロが n個の場合の和
平均
μn+ = E[ x1 + x2 + … + xn ] = E[ x1 ] + E[ x2 ] + … + E[ xn ] = n E[ x1 ] = n・(7/2)
準備
E[ x1x2 … xn ] = (1/6)n × { Σi=1~6 i }n = (21/6)n = (7/2)n
E[ (x1 + x2 + … + xn)2 ] = n E[ x12 ] + 2・nC2・E[ x1x2 ] = n・(91/6) + n・(n-1)・(49/4)
分散
Vn+ = E[ (x1 + x2 + … + xn)2 ] - E[ x1 + x2 + … + xn ]2 = n・(91/6) + n・(n-1)・(49/4) - n2・(49/4) = n・(35/12)
標準偏差 σn+ = √Vn+ = √(35n/12)
サイコロを複数個 (または複数回) 振った場合の目の積
サイコロが2個の場合の積
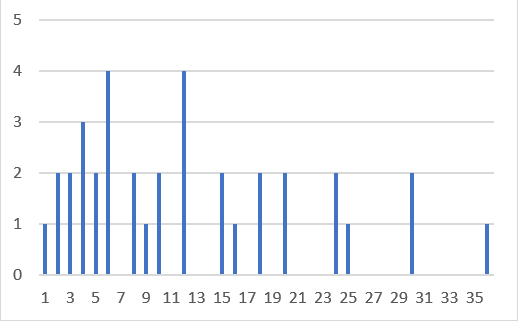
平均
μ2x = E[ x1x2 ] = (1/36) × Σi=1~6 { Σj=1~6 ( i × j ) }
= (1/36) × Σi { i × Σj j }
= (1/36) × Σi { 21・i }
= (1/36) × 21 × 21 = 49/4
準備
E[ (x1x2)2 ] = (1/36) × Σi=1~6 { Σj=1~6 ( i × j )2 }
= (1/36) × Σi { i2 × Σj j2 }
= (1/36) × Σi { 91・i }
= (1/36) × 91 × 91 = 8281/36
分散
V2x = E[ (x1x2)2 ] - E[ x1x2 ]2 = 8281/36 - (49/4)2 = 11515/144
標準偏差 σ2x = √V2x = √(11515/144)
一般化 サイコロが n個の場合の積
平均
μnx = E[ x1x2 … xn ] = (1/6)n × { Σi=1~6 i }n = (21/6)n = (7/2)n
準備
E[ (x1x2 … xn)2 ] = (1/6)n × { Σi=1~6 i2 }n = (91/6)n
分散
Vnx = E[ (x1x2 … xn)2 ] - E[ x1x2 … xn ]2 = (91/6)n - { (7/2)n }2 = (91/6)n - (49/4)n
標準偏差 σnx = √Vnx = √{ (91/6)n - (49/4)n }