Top　　関連リンク 前回 [すごろくでサイコロを何回振ればゴールできるか? マス数とターン数の関係]　,　[サイコロが2個の場合]

---

続・すごろくでサイコロを何回振ればゴールできるか?　分散・標準偏差

前回 は、すごろくでゴールするまでにサイコロを振る回数の期待値を求めた。
今回は分散・標準偏差を計算する。途中は全て分散で計算し、最後に標準偏差を計算する。
すごろくのルールなどは前回に準ずる。

変数

使用する変数が増えるので前回と変数の割り当てを変える。
サイコロを振る回数の確率変数を x_i とする。x の期待値を 期待値を E[x]、分散を V[x] とする。
マスをゴールから近い順に q_i とする。

6マスのすごろく

最初に6マス(ゴールを含まない)しかない短いすごろくで考える。


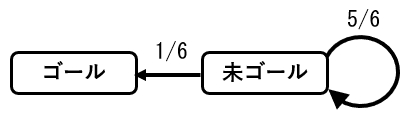
前述した通り、この場合はどの位置でもある値が出ればゴールできる状態になっている(確率 1/6)。
出なければ、引き続きサイコロを振る状態に戻る(確率 5/6)。
ゴールまでにサイコロを振る回数の期待値は、開始位置によらず E[x] = 6 である。

分散 V[x] を計算する。分散の公式より、
V[x] = E[x²] - { E[x] }²
第2項は 6² = 36 と分かっているので、第1項を計算する。
E[x²] = (1/6)・1² + (1/6)・(5/6)・2² + (1/6)・(5/6)²・3² + (1/6)・(5/6)³・4² + …

これを解くと、E[x²] = 66 となる。よって、分散 V[x] = 30、標準偏差 σ = √30 ≈ 5.48となる。
平均 6 に対して標準偏差が約 5.48 なので、ゴールまでの回数は結構ばらつくことがわかる。

nマスのすごろく

次に nマス(n≧7)に一般化するのだが、n = 7 の場合だけは少し特殊なので言及しておく。

先に答えを言うと 期待値 E[x₇] = 7, 分散は 6マスと同じで V[x₇] = 30 である。
理由は 7マスの場合は、1回目のサイコロを振った後に 100% の確率で 6マスのすごろくの状態になるからである。

では、一般の場合について考える。n≧7なので、ゴールからの跳ね返りは考慮しなくてよい。一方通行である。
V[x_n] = E[x_n²] - { E[x_n] }²
第2項は前回計算したので、第1項を計算する。

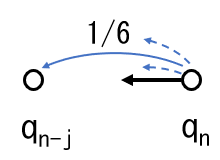
スタートでサイコロを振ると、q_n から 1/6 の確率で q_n-j ( 1≦j≦6 ) に移る。
ゴールまでの回数 x_n は x_n-j に 1 加算される。(α+1)² = α² + 2 α + 1 であることを考慮すると、
E[x_n²] = Σ(1/6)・{ E[x_n-j²] + 2 E[x_n-j] + 1 } 　　　( j=1 to 6 )
= (1/6)・Σ{ V[x_n-j] + { E[x_n-j] }² + 2 E[x_n-j] + 1 } 　　　( j=1 to 6 )

よって、分散 V[x_n] は次式で漸化的に計算することができる。
V[x_n] = (1/6)・Σ{ V[x_n-j] + { E[x_n-j] }² + 2 E[x_n-j] + 1 } - { E[x_n] }² 　　　( j=1 to 6 )

なお次のように、この式は最初に言及した n = 7 の場合も含んでいる。
V[x₇] = (1/6)・Σ{ V[x_7-j] + { E[x_7-j] }² + 2 E[x_7-j] + 1 } - { E[x₇] }² 　　　( j=1 to 6 )
= (1/6)・Σ{ 30 + 6² + 2 × 6 + 1 } - 7² 　　　( j=1 to 6 )
= 30

下の表は上式で計算した ゴールまでにサイコロを振る回数の期待値、分散、標準偏差である。
マス数 n = 1000 でも回数の標準偏差は約 10 である。マス数の増加に対して、回数のばらつきの増加は緩慢である。
この理由を定性的に説明すると次のようになる。
マス数が大きくなるとサイコロを振る回数自体が増える。すると大数の法則で、出る目の平均のばらつきが減少する。
そのため、ゴールまでの回数はそれ程ばらつかないのである。

すごろくのマスの数 (ゴールを含まない) n	サイコロを振る回数の期待値 E[xn]	分散 V[xn]	標準偏差 σn
6	6	30	5.477
7	7	30	5.477
8	7.167	30.139	5.49
9	7.361	30.286	5.503
10	7.588	30.427	5.516
11	7.853	30.538	5.526
12	8.161	30.577	5.53
13	8.522	30.486	5.521
14	8.775	30.624	5.534
15	9.043	30.738	5.544
16	9.324	30.823	5.552
17	9.613	30.882	5.557
18	9.906	30.924	5.561
19	10.197	30.971	5.565
20	10.476	31.065	5.574
21	10.76	31.142	5.581
22	11.046	31.209	5.587
23	11.333	31.271	5.592
24	11.62	31.333	5.598
25	11.905	31.402	5.604
26	12.19	31.476	5.61
27	12.476	31.544	5.616
28	12.762	31.611	5.622
29	13.048	31.677	5.628
30	13.333	31.745	5.634
31	13.619	31.814	5.64
32	13.905	31.883	5.646
33	14.19	31.95	5.652
34	14.476	32.018	5.658
35	14.762	32.086	5.664
36	15.048	32.154	5.67
37	15.333	32.222	5.676
38	15.619	32.29	5.682
39	15.905	32.358	5.688
40	16.19	32.426	5.694
41	16.476	32.494	5.7
42	16.762	32.562	5.706
43	17.048	32.63	5.712
44	17.333	32.698	5.718
45	17.619	32.766	5.724
46	17.905	32.834	5.73
47	18.19	32.902	5.736
48	18.476	32.971	5.742
49	18.762	33.039	5.748
50	19.048	33.107	5.754
51	19.333	33.175	5.76
52	19.619	33.243	5.766
53	19.905	33.311	5.772
54	20.19	33.379	5.777
55	20.476	33.447	5.783
56	20.762	33.515	5.789
57	21.048	33.583	5.795
58	21.333	33.651	5.801
59	21.619	33.719	5.807
60	21.905	33.787	5.813
61	22.19	33.855	5.818
62	22.476	33.923	5.824
63	22.762	33.991	5.83
64	23.048	34.059	5.836
65	23.333	34.127	5.842
66	23.619	34.195	5.848
67	23.905	34.263	5.853
68	24.19	34.331	5.859
69	24.476	34.399	5.865
70	24.762	34.467	5.871
71	25.048	34.535	5.877
72	25.333	34.603	5.882
73	25.619	34.671	5.888
74	25.905	34.739	5.894
75	26.19	34.807	5.9
76	26.476	34.875	5.906
77	26.762	34.943	5.911
78	27.048	35.011	5.917
79	27.333	35.079	5.923
80	27.619	35.147	5.929
81	27.905	35.215	5.934
82	28.19	35.283	5.94
83	28.476	35.351	5.946
84	28.762	35.42	5.951
85	29.048	35.488	5.957
86	29.333	35.556	5.963
87	29.619	35.624	5.969
88	29.905	35.692	5.974
89	30.19	35.76	5.98
90	30.476	35.828	5.986
91	30.762	35.896	5.991
92	31.048	35.964	5.997
93	31.333	36.032	6.003
94	31.619	36.1	6.008
95	31.905	36.168	6.014
96	32.19	36.236	6.02
97	32.476	36.304	6.025
98	32.762	36.372	6.031
99	33.048	36.44	6.037
100	33.333	36.508	6.042
…	…	…	…
1000	290.476	97.732	9.886
…	…	…	…
10000	2861.905	709.977	26.645